月: 2024年10月

こんばんは、スタッフのUです。

今回は算数の平面図形の求積の問題を。

問題

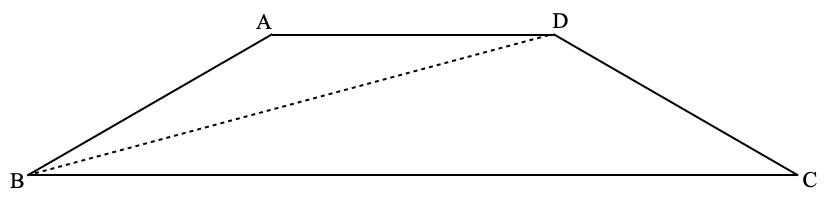
下の四角形ABCDは、BA＝AD＝DCで，∠BAC＝∠ADC＝150°，∠ABC＝∠BCD＝30°、対角線BDの長さが2cmの等脚台形です。四角形ABCDの面積を求めてください。

中学数学の三平方の定理や高校数学の三角比などの知識を駆使していただいてもかまいませんが、

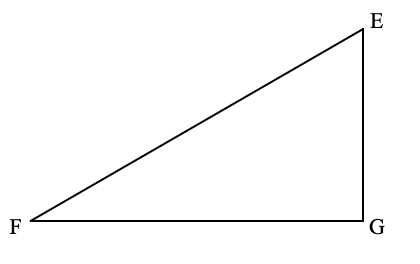
上図の、∠E＝60°，∠F＝30°，∠G＝90°の直角三角形(三角定規の一つの形)でFE : EG＝2 : 1となることを知っていれば、三平方の定理や三角比を使わずとも算数の知識で解くことができます(つまり答えに平方根は出てきません)。

一度考えてみてください。解答は次回に。

こんばんは、スタッフのUです。

昨日、染織ブランドアトリエシムラ代表の志村昌司さんのXのポストで、染織家の志村ふくみさんが百歳を迎えたことを知りました（昌司さんはふくみさんのお孫さんです）。

そこで、日本の百歳以上の方（センテナリアン）の人口を調べてみると2024年9月17日時点で95,119人で、去年の9月15日時点での92,139人から2,980人増加しているそうです。

「百歳」といえば私などはどうしても、百歳超の双子として一時期メディアなどでも引っ張りだこだった「きんさん・ぎんさん」のことを思い出すのですが、きんさん・ぎんさんが百歳を迎えたのが1992年で、その当時の日本の百歳以上の人口が4,152人。日本の人口は1992年と今でほとんど変わりませんので(1992年が1.244億人、2024年が1.248億人)、このように見てみても日本社会の高齢化が激しい勢いで進んでいることがよくわかります。

社会の仕組みもそれに応じて速やかに変わっていかなければならないところですが、私たちもそのような社会の変化を視野に入れつつ仕事を進めていこうと思います。