こんばんは、スタッフのUです。
前回、平面図形の求積の問題を出題しました(内容はこちらでご確認ください)ので、今回は「解答編」です。
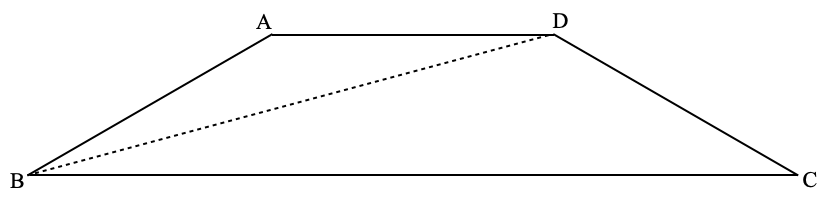
この問題を、三角比などを使わず受験算数の知識だけで解く上での大きなヒントは、仮定にある「BA=AD=DCで,∠BAC=∠ADC=150°」です。辺の長さと内角が等しいということで「正多角形の一部を切り取った図形」の可能性に気付けばしめたものです。一つの内角が150°の正多角形は正十二角形ですので1)、この四角形ABCDは下図のような正十二角形の一部を切り取った図形だとわかります。

この正十二角形に外接する円と、円の中心Oと各頂点を結んだ半径を書き込むと下図のようになり、正十二角形が頂角30°の二等辺三角形2)12個に分割できます。
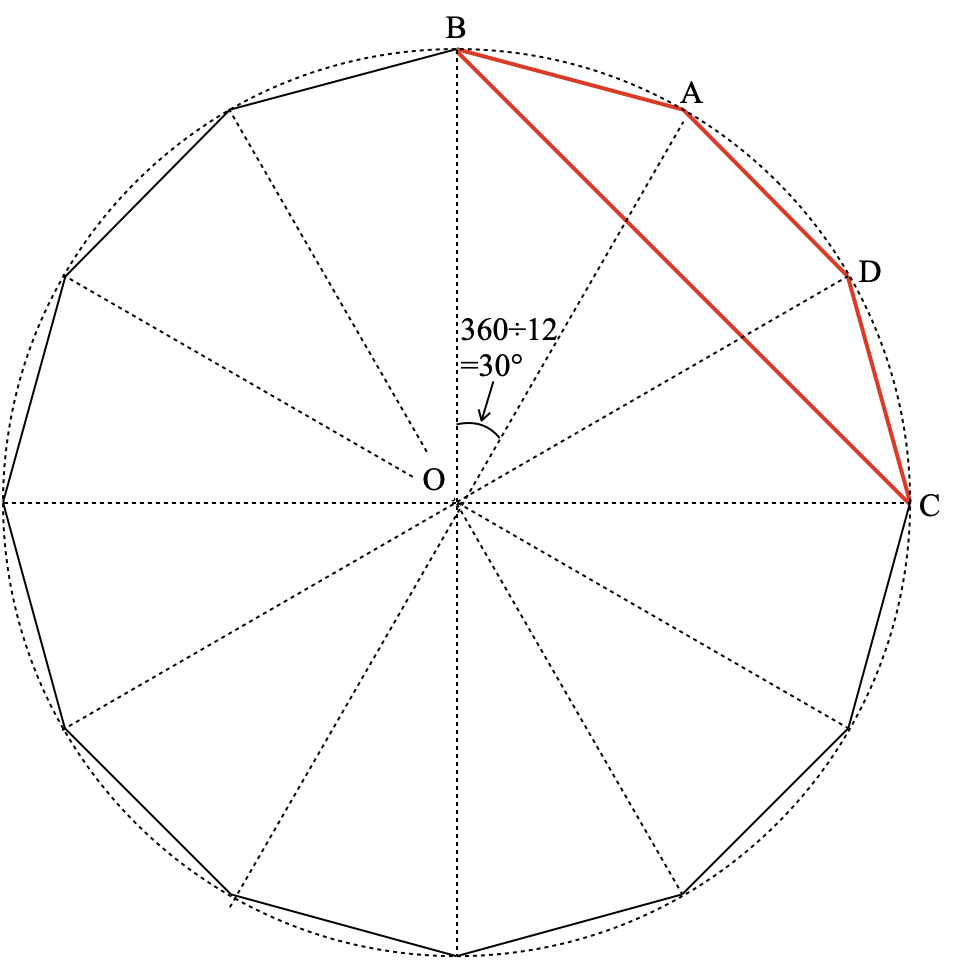
すると四角形ABCDの面積は、下図の緑の二等辺三角形3つの面積の合計から、黄色の三角形OBCの面積を引いて求めることができます。しかし、それらの面積を求めるためにはこの円の半径の長さがわからなければなりません。
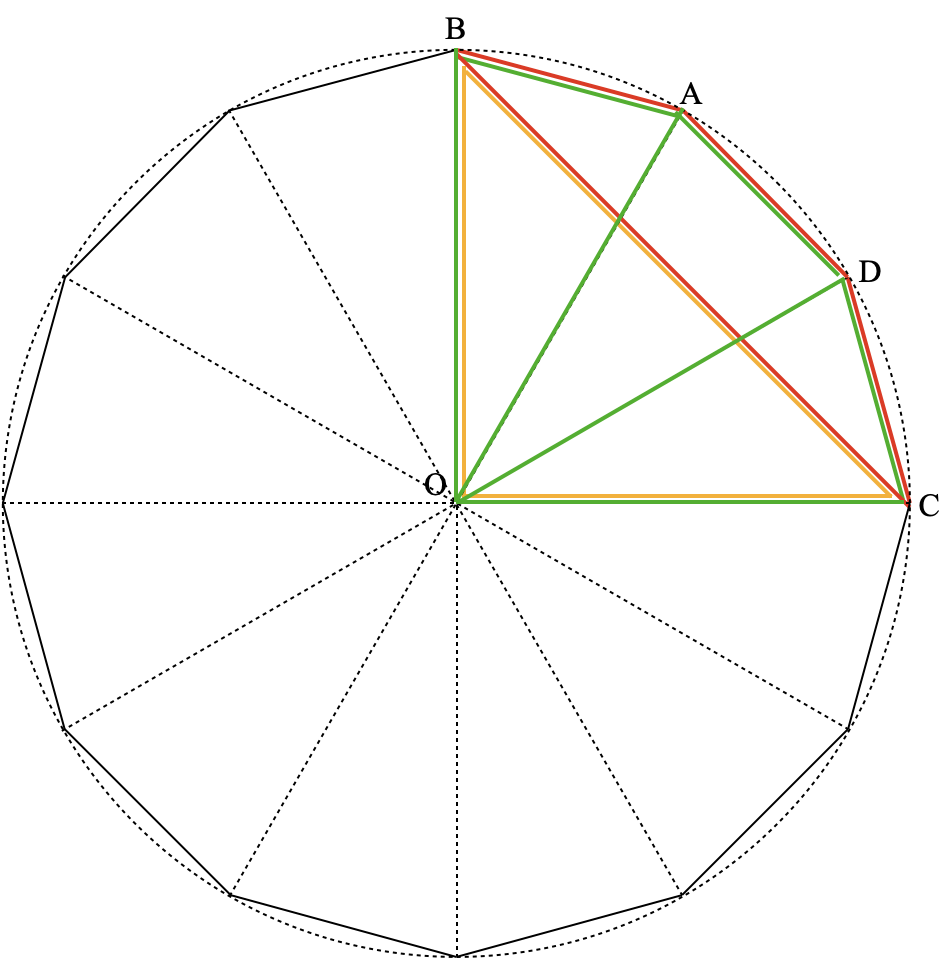
そこで問題文のもう一つの仮定に注目すると「対角線BDの長さが2cm」とあります。円の中心Oと頂点B,Dを結んでできる三角形OBDは頂角の∠BODが60°の二等辺三角形、つまり正三角形になります3)ので、この円の半径はBDの長さと等しく2cmだとわかります。
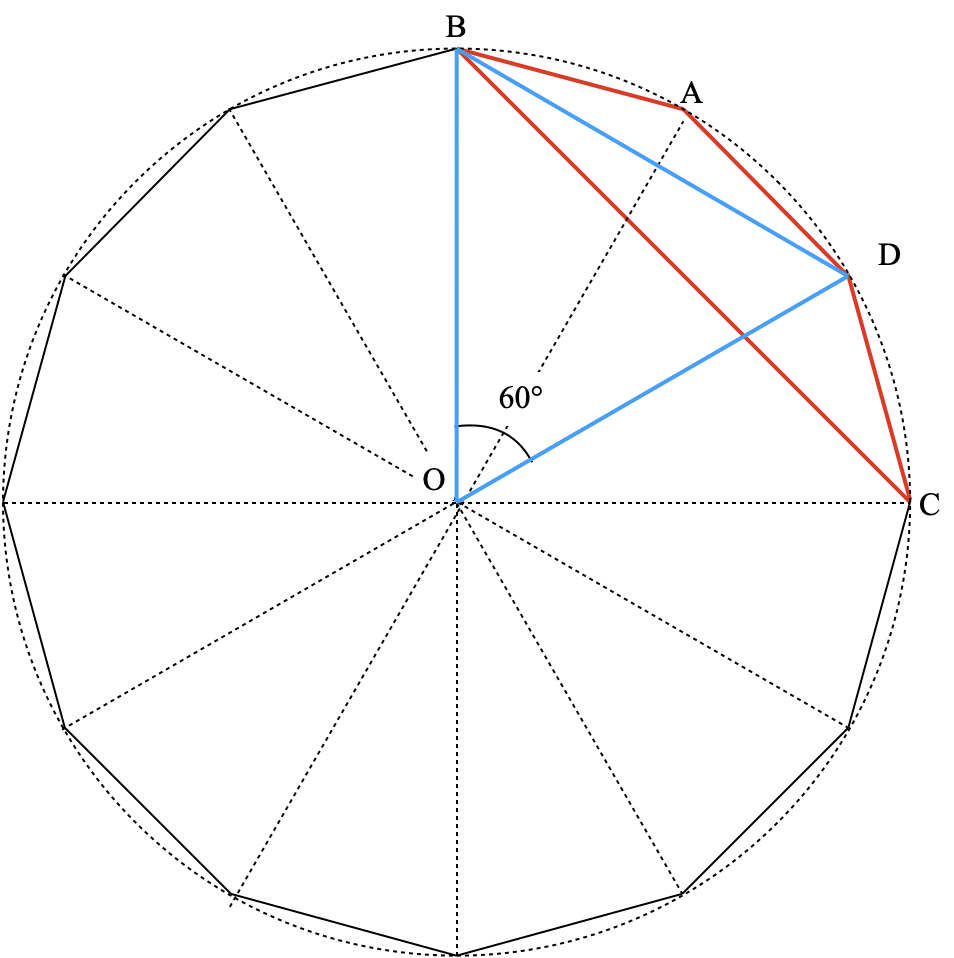
また二つ上の図の緑の二等辺三角形3つの面積ですが、1つの形は下図のようになっていますので、
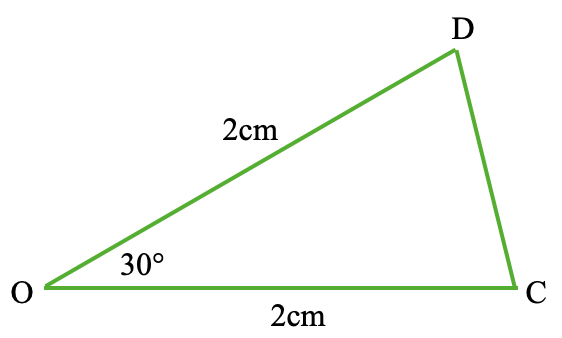
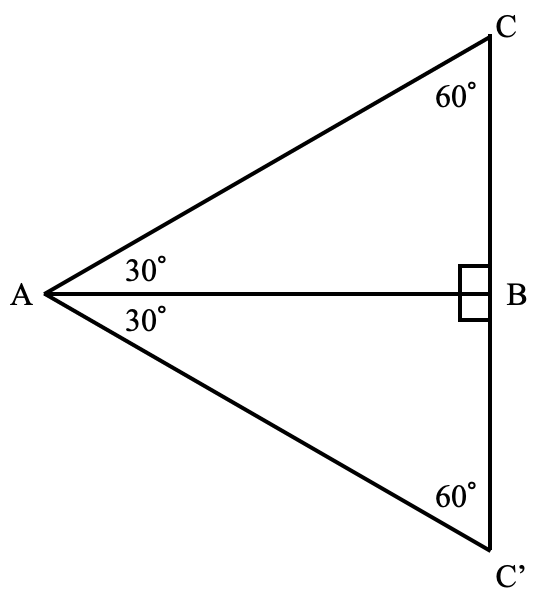
DからOCに垂線を引きその足をHとすると、下図のように内角が30°,60°,90°の三角定規の形の直角三角形ができます。前回ヒントとして記したように、DHの長さはDOの長さの半分4)ですので、1cmとわかります。
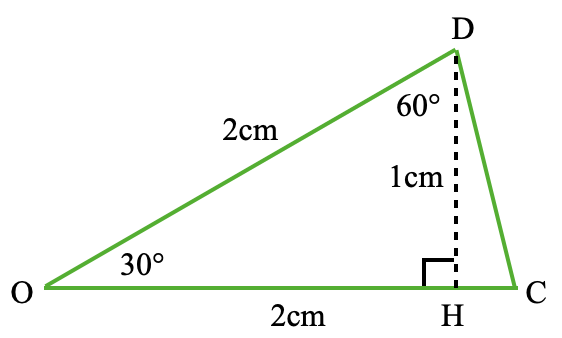
よって緑の二等辺三角形1つの面積は2×1÷2=1(cm2)とわかります。
また黄色の三角形OBCは直角を挟む二つの辺の長さが2cmの直角二等辺三角形なので、面積は2×2÷2=2(cm2)です。
以上より、求める四角形ABCDの面積は、
(緑の二等辺三角形3つの面積の合計)-(黄色の三角形OBCの面積)
なので、1×3-2=1(cm2)
です。
いかがでしょうか。
仕事の合間の息抜きに、頭をできるだけ使わず休めるようにするのもいいですが、たまにはこのように別の頭の使い方をしてみてもよい刺激になるかもしれません。
1) ある正多角形の一つの内角が150°ならば、一つの外角は180°-150°=30°です。正多角形の外角の和は360°なので、一つの外角が30°の正多角形は360°÷30°=12で正十二角形とわかります。
2) 例えば図の三角形OABはOAとOBがいずれも円の半径で等しいので二等辺三角形です。
3) 頂角が60°の二等辺三角形の二つの底角は(180-60)÷2=60°で、3つの内角がすべて等しいので正三角形です。
4) 下図のように3つの内角が30°,60°,90°の直角三角形ABCに、ABを対称軸として線対称な三角形ABC’を描き加えると、三角形ACC’はすべての内角が60°なので正三角形です。そこでBCの長さを1とすると、CC’はBCの長さの倍の2となり、それがこの正三角形の一辺の長さ(CC’,AC,AC’)なので、ACとBCの長さの比は2:1となります(これは、中学受験の進学塾などでは教えている知識です)。